Certain mathematical equations open unique windows to the outside world. They help to better understand reality and realize things that until recently were something out of the ordinary. Many of them really influenced the course of history and even changed the world around them.
Pythagoras’ theorem (BC)
One of the key trigonometric rules. It’s about the aspect ratio of a right-angled triangle. The sum of the length of each of the two shorter sides squared is equal to the length of the longest side in the second power. The equation not only found applications in construction, navigation, cartography and other important processes, but also helped to expand the significance of the very concept of numbers. Interestingly, the followers of Pythagoras, who were engaged in mathematics, were even subject to persecution, because such knowledge was always frightening for the ignorant.
The law of universal gravitation (1687)
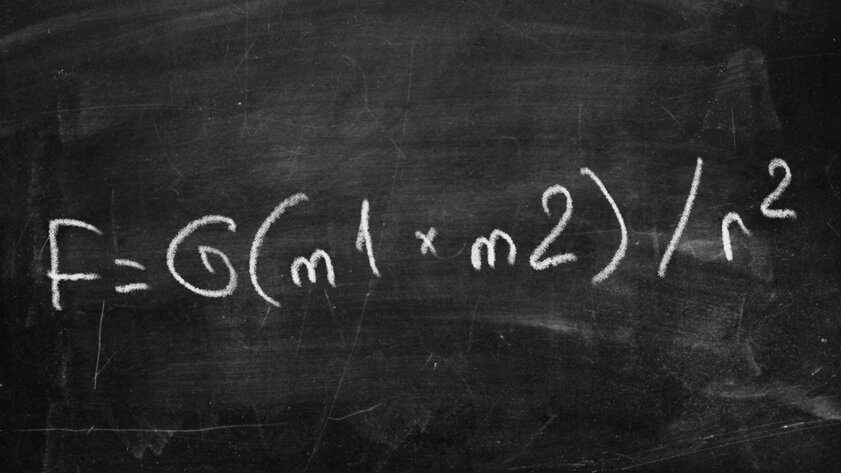
Isaac Newton was the author of this equation. He first came up with the second law of motion, which states that force is equal to the mass of an object times its acceleration. Expansion of understanding of this discovery closer to 1687 led to the creation of the law of universal gravitation. Until today, it has been used to understand many physical systems, including the motion of planets in the solar system and the ability to travel between them using rockets. Roughly speaking, if not for this equation, today there might not be SpaceX and other similar companies that are aimed at conquering space.
The Wave Equation (1743)
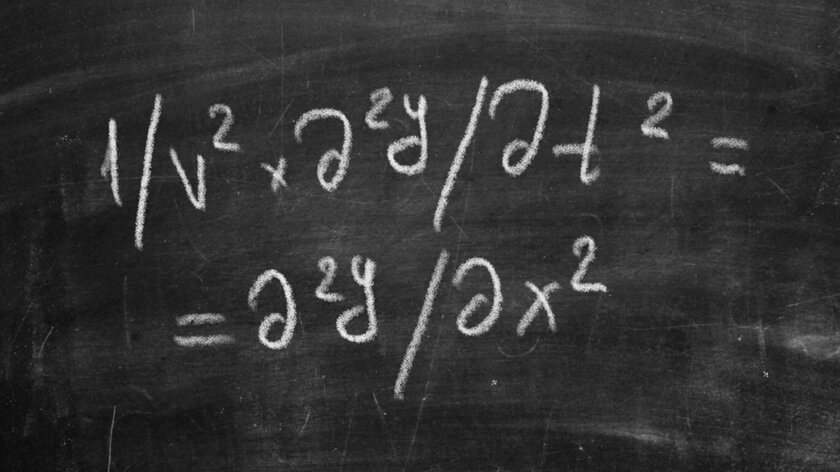
Under the inspiration of Newton’s activities, scientists of the 18th century began to analyze absolutely everything that surrounded them. The activity of the French polymath Jean-Baptiste le Ronda d’Alembert, who in 1743 derived an equation describing the motion of a wave, turned out to be important. When expanded to two or more dimensions, the wave equation enables researchers to predict the direction of water flow and analyze seismic activity and sound waves. Research in the category of quantum physics, based on the wave equation, is also important. It should be understood that it, among other things, is the basis for many processes that occur in modern electronics.
Square Root of -1 (1750)
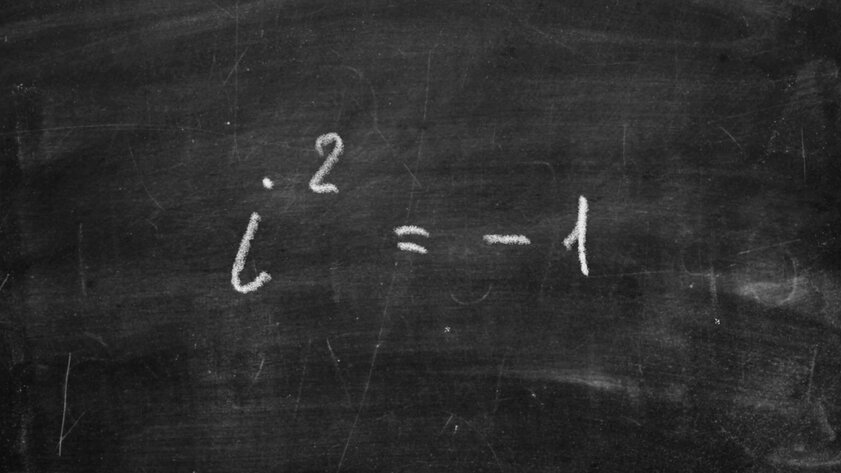
It seems that the square root of -1 is something irrational, because there cannot be two identical numbers, the product of which will give a negative value. Yes, that is right. However, the value of Leonard Euler, which is usually denoted as i, gives an understanding of complex numbers, which is very important for modern electronics.
Fourier’s equation (1822)
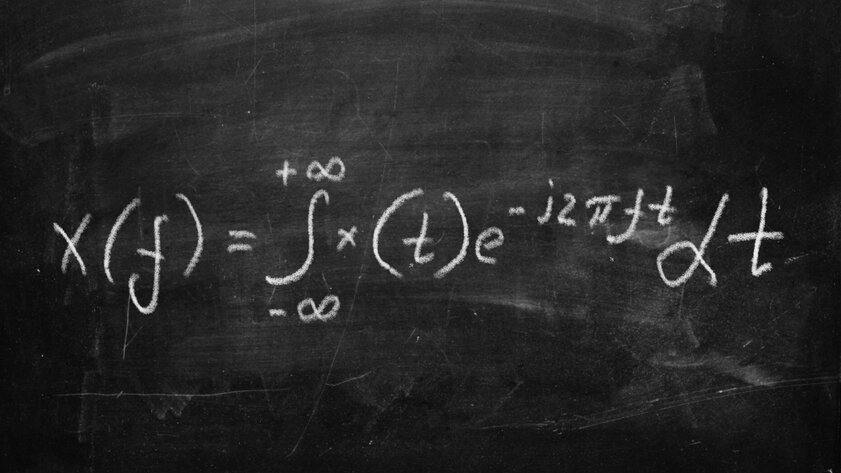
It is unlikely that many who came across this material heard about Jean-Baptiste Joseph Fourier, but his equation definitely influenced everyone’s life. It made it possible to break down complex and messy datasets into combinations of simple ones that are much easier to analyze. Many scientists immediately refused to believe that really cumbersome mathematical systems could be so elegantly reduced. But eventually Fourier’s work became the foundation of many modern fields of science, including data processing, image analysis, optics, communications, astronomy, and engineering.
Navier-Stokes equations (1845)
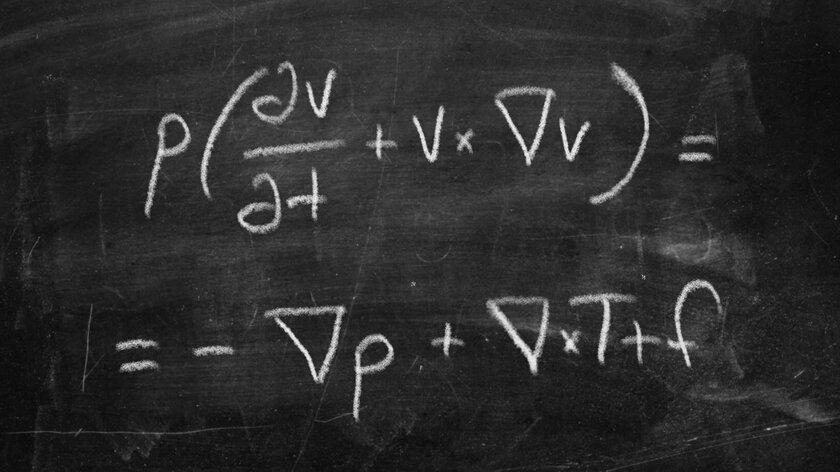
Like a wave, this Navier-Stokes differential equation describes the behavior of liquids and other substances: water that moves through a pipe, milk added to coffee, air currents over the wing of an airplane, smoke rising up from a lit cigarette. It is with the help of the Navier-Stokes equations in modern three-dimensional graphics that fluid motion is modeled very well.
Maxwell’s equations (1864)
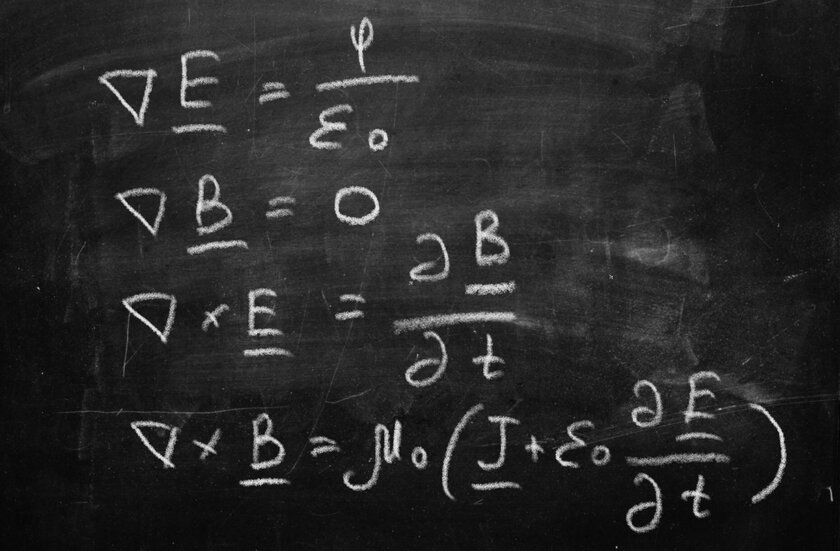
Electricity and magnetism were fairly new concepts in the 1800s – then scientists were just beginning to capture and use these strange forces. However, the Scottish researcher James Clerk Maxwell significantly expanded the understanding of such phenomena and in 1864 presented a list of two dozen equations that described the functioning of electricity and magnetism, as well as the relationship between them. Until today, four key equations have reached, which are still taught to physics students and serve as the basis for absolutely all electronics from the world around us.
Second Law of Thermodynamics (1874)
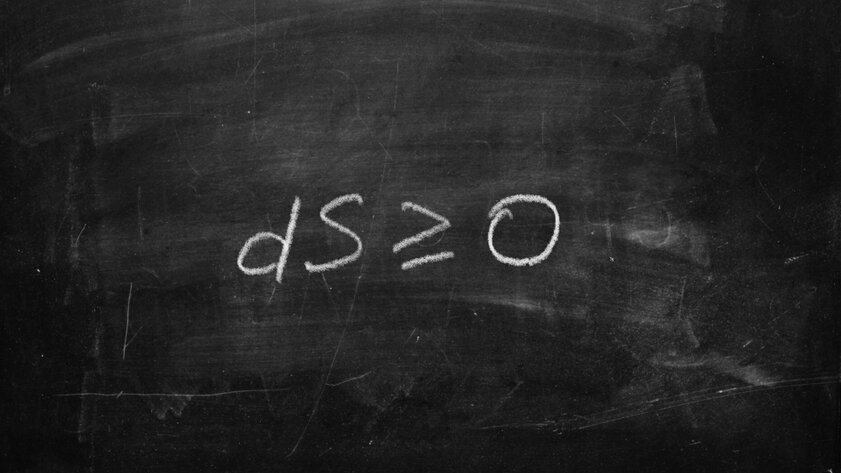
Ludwig Boltzmann’s second law of thermodynamics is an important physical precedent in which the passage of time is paramount. The fact is that the vast majority of physical processes are reversible: we can run the equations in reverse order and get the opposite result. But this law only works in one direction. For example, if we place an ice cube in a cup of hot coffee, we will see exactly how it melts. But it is impossible to even imagine that the opposite result is possible – it is simply impossible to get an ice cube from hot coffee in its original form.
The theory of relativity (1905)
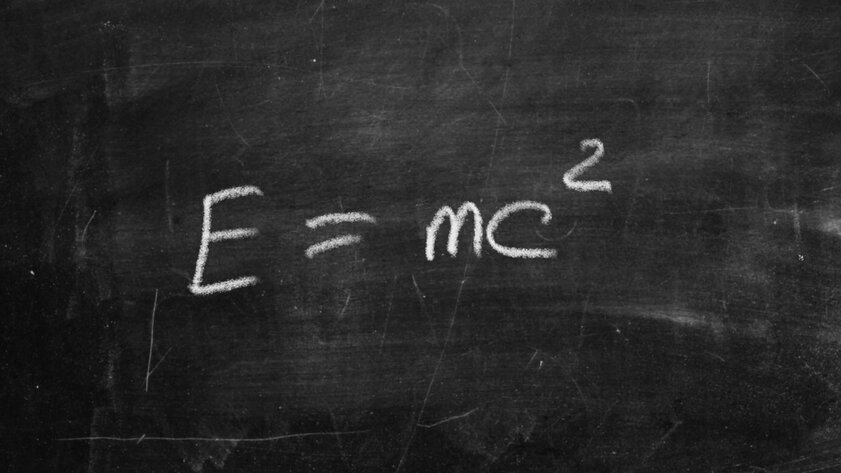
The author of this equation was Albert Einstein. He confirmed that matter and energy are a pair of aspects of the same whole. The equation uses mass, energy, and constant speed of light. For many, it remains far from the easiest to understand. However, it is very important to know that without this mathematical law, scientists would not be able to understand exactly how individual stars and the entire Universe function. Moreover, giant particle accelerators like the Large Hadron Collider, which are actively used in understanding the world at the subatomic level, would also not be possible without just a couple of variables, the relationship of which was formulated by Einstein.
Friedman’s equations (1922)
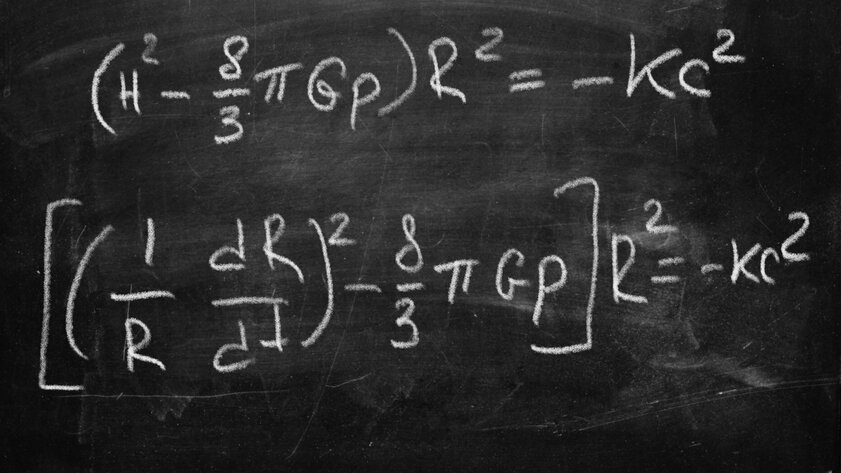
It would be arrogant to even think that you can create a set of equations that can explain the entire cosmos at once. However, in the 1920s, Russian physicist Alexander Fridman did just that. Using Einstein’s theory of relativity, Freudman showed that the characteristics of the expanding universe can be expressed, starting with the Big Bang, using just two equations. They combine all the important aspects of the cosmos, including its curvature, the amount of matter and energy, as well as the expansion rate and a number of other key constants, including the speed of light, the gravitational constant, and so on.
Shannon’s Information Equation (1948)
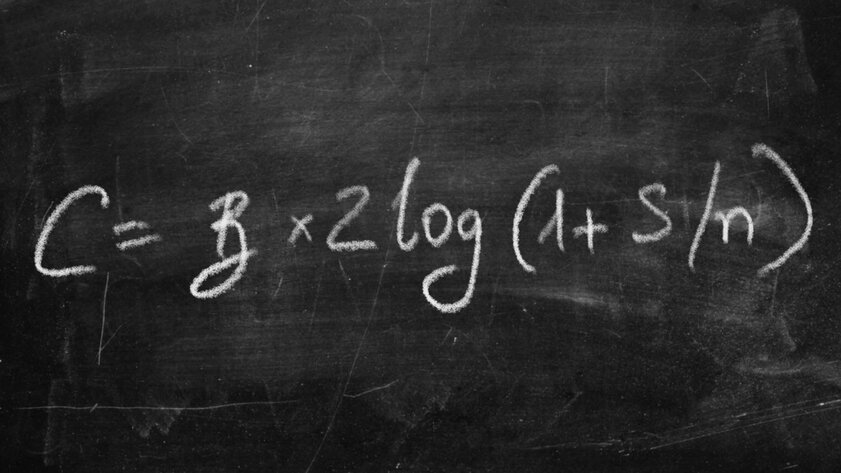
Claude Shannon outlined an equation showing the maximum efficiency with which information can be transmitted. The output of the equation is expressed in bits per second. Yes, at that time he already had an understanding of this quantity, which eventually became very important in the binary system. Of course, if it were not for him, someone else might have been studying all this. However, it is much more interesting to realize that it was Shannon who became the father of the digital era, which simply would not have been possible without him. It can be assumed that the activities of a scientist half a century ago determined the banal opportunity to read this text.
May Logistics Map (1976)
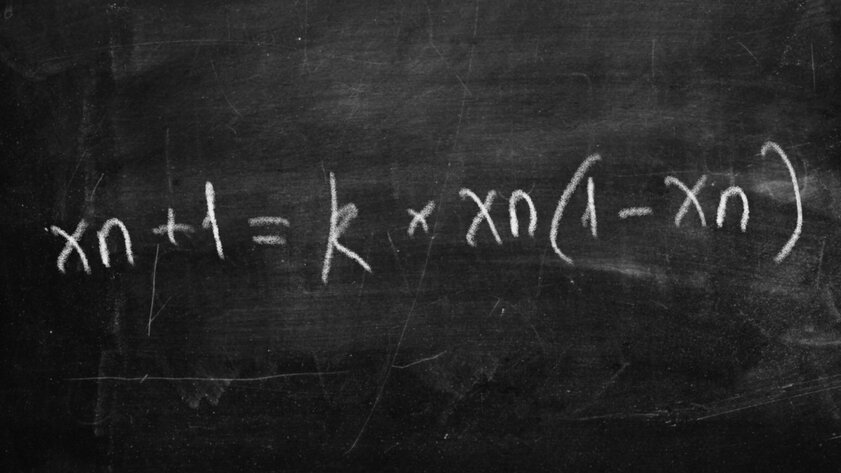
This equation was popularized by Australian physicist, mathematician and ecologist Robert May. It gives an understanding of exactly how the general system will look at the next moment in time. It seems that in such mathematical work there is absolutely nothing complicated, but in practice it is not. The behavior can be as chaotic as possible, therefore, the future state of the system can be very different. May’s equation eventually began to be used to explain the dynamics of population growth in biology, as well as to generate random numbers in programming.
Sources: LiveScience, Business Insider.
Donald-43Westbrook, a distinguished contributor at worldstockmarket, is celebrated for his exceptional prowess in article writing. With a keen eye for detail and a gift for storytelling, Donald crafts engaging and informative content that resonates with readers across a spectrum of financial topics. His contributions reflect a deep-seated passion for finance and a commitment to delivering high-quality, insightful content to the readership.







